Breaking New Ground in Stock Market Prediction: The ATLAS-CNN Architecture

Breaking New Ground in Stock Market Prediction: The ATLAS-CNN Architecture

Predicting stock market movements has long been considered one of the most challenging applications of machine learning. Today, I'm excited to share our recent work on ATLAS-CNN, a novel deep learning architecture that achieves 73-75% directional accuracy in stock market prediction - a significant improvement over traditional approaches that typically hover around 60%.

This work has been published on SSRN and is currently under review at Expert Systems with Applications (ESWA).

The Challenge of Market Prediction

Why is predicting the stock market so difficult? Markets are incredibly complex systems influenced by countless factors - from company performance and economic indicators to global events and human psychology. Traditional machine learning approaches often struggle to capture these intricate relationships and fail to maintain consistent performance across different market conditions.

Enter ATLAS-CNN

Our approach combines the pattern-recognition capabilities of Convolutional Neural Networks (CNNs) with the temporal modeling strengths of Long Short-Term Memory (LSTM) networks in a novel way. But what makes ATLAS-CNN different isn't just that it combines these techniques - it's how it does so.

Figure 1: Overall architecture of ATLAS-CNN showing the integration of CNN and LSTM branches with the TMDO operator

The Secret Sauce

ATLAS-CNN introduces three key innovations:

1. A New Way to Look at Market Data

Instead of treating financial data as simple time series, we transform it into a 2D image-like format. This allows us to capture relationships between different market indicators in a way that's similar to how CNNs process images.

Figure 2: Data organization and multi-scale CNN architecture showing how financial time series are transformed into a 2D format

2. Smart Pattern Recognition

We use specialized convolution kernels designed specifically for different types of market patterns:

• Long-term trend kernel (3×50) for quarterly market trends
• Pattern recognition kernel (5×25) for technical chart patterns
• Market dynamics kernel (7×15) for capturing liquidity patterns

3. The TMDO Operator

The Temporal Multi-Dimensional Operator (TMDO) is our mathematical framework for capturing how different market indicators influence each other over time.

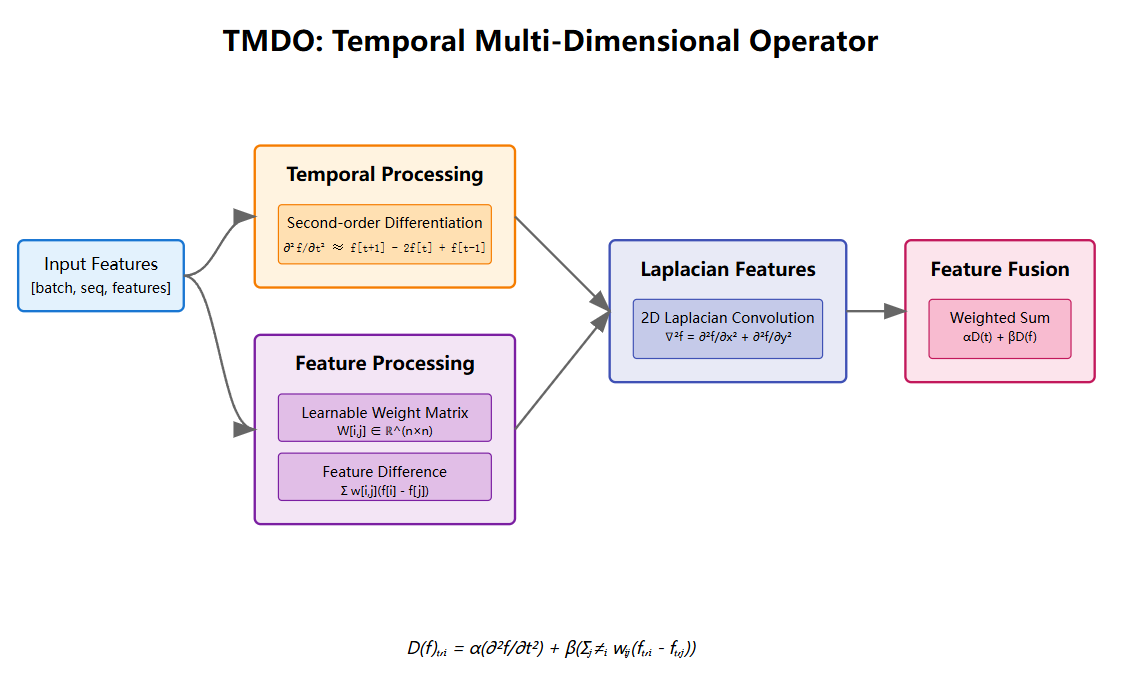
Figure 3: TMDO architecture illustrating how temporal and spatial market data relationships are processed

Real-World Performance

The results have been remarkable. Let's look at the performance metrics:

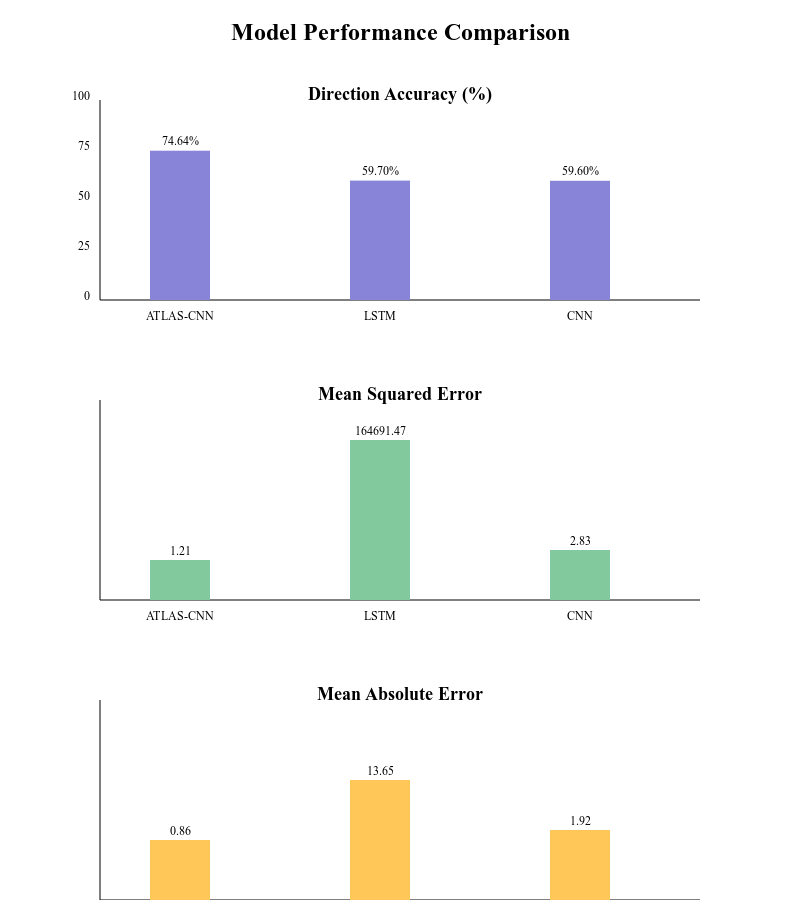
Figure 4: Performance comparison across different market conditions

Key achievements include:

• 73-75% directional accuracy across different stocks
• Strong performance during high volatility (72.3% accuracy during the COVID-19 crash)
• 89% accuracy in capturing the impact of earnings announcements
• Low latency (8.5ms) making it suitable for real-world trading applications

What's particularly impressive is the model's stability during market volatility:

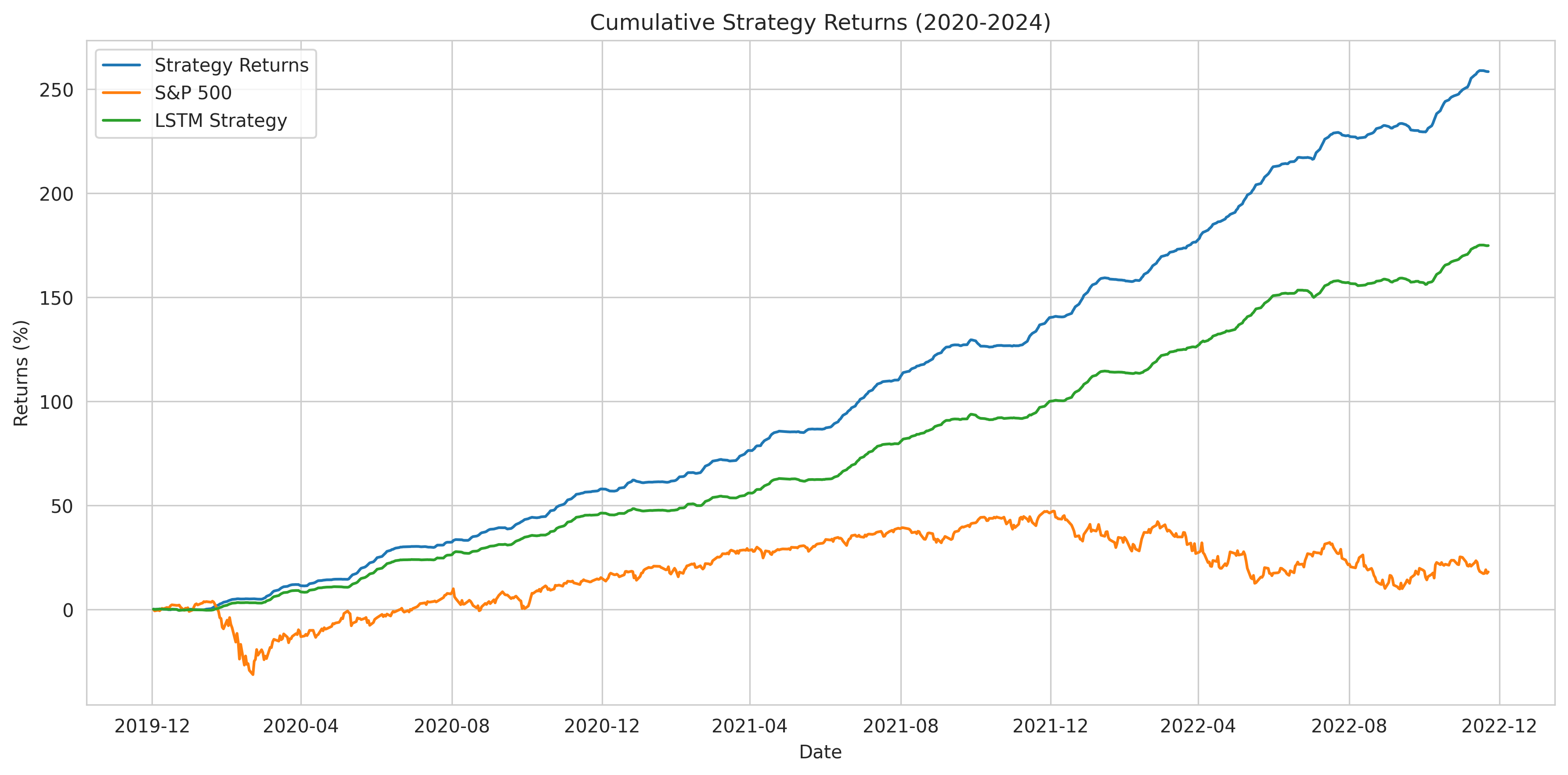
Figure 5: Cumulative returns comparison showing consistent performance

The Technical Foundation: A Deep Dive

Function Spaces and Core Definitions

We begin by defining our domain Ω = [0,T] × {1,...,N}, where T represents our time horizon and N is the number of market indicators. We work in two key function spaces:

1. L²(Ω) with norm:

2. H²(Ω) as the Sobolev space with norm:

The TMDO Operator

The heart of ATLAS-CNN is the Temporal Multi-Dimensional Operator (TMDO). This operator, D: H²(Ω) → L²(Ω), is defined as:

Where:

• The first term captures temporal dynamics through second-order differentiation
• The second term models inter-indicator relationships through weighted differences
• α, β ∈ [0.3,0.7] control the balance between temporal and spatial effects
• wij forms a stochastic matrix (∑j wij = 1) representing learned relationships between indicators

Key Theoretical Properties

1. Well-Posedness (Theorem 3.1):
   For given initial conditions f(0,i), ∂tf(0,i), the TMDO evolution problem has a unique solution in H²(Ω) under standard market conditions.

2. Convergence (Theorem 3.2):
   Under appropriate conditions on α and β, TMDO is a contraction mapping:

   \|D(f) - D(g)\|_{L^2(\Omega)} \leq C(\alpha + \beta)\|f - g\|_{H^2(\Omega)}

3. Stability (Theorem 3.3):
   The discrete TMDO implementation is stable under the CFL-like condition:

   \alpha\Delta t^2 < 4 \text{ and } \beta\Delta t^2|\lambda_k| < 2

Error Analysis

The global error Eⁿ at time step n satisfies:

This bound comes from combining local truncation error bounds with the discrete Gronwall inequality.

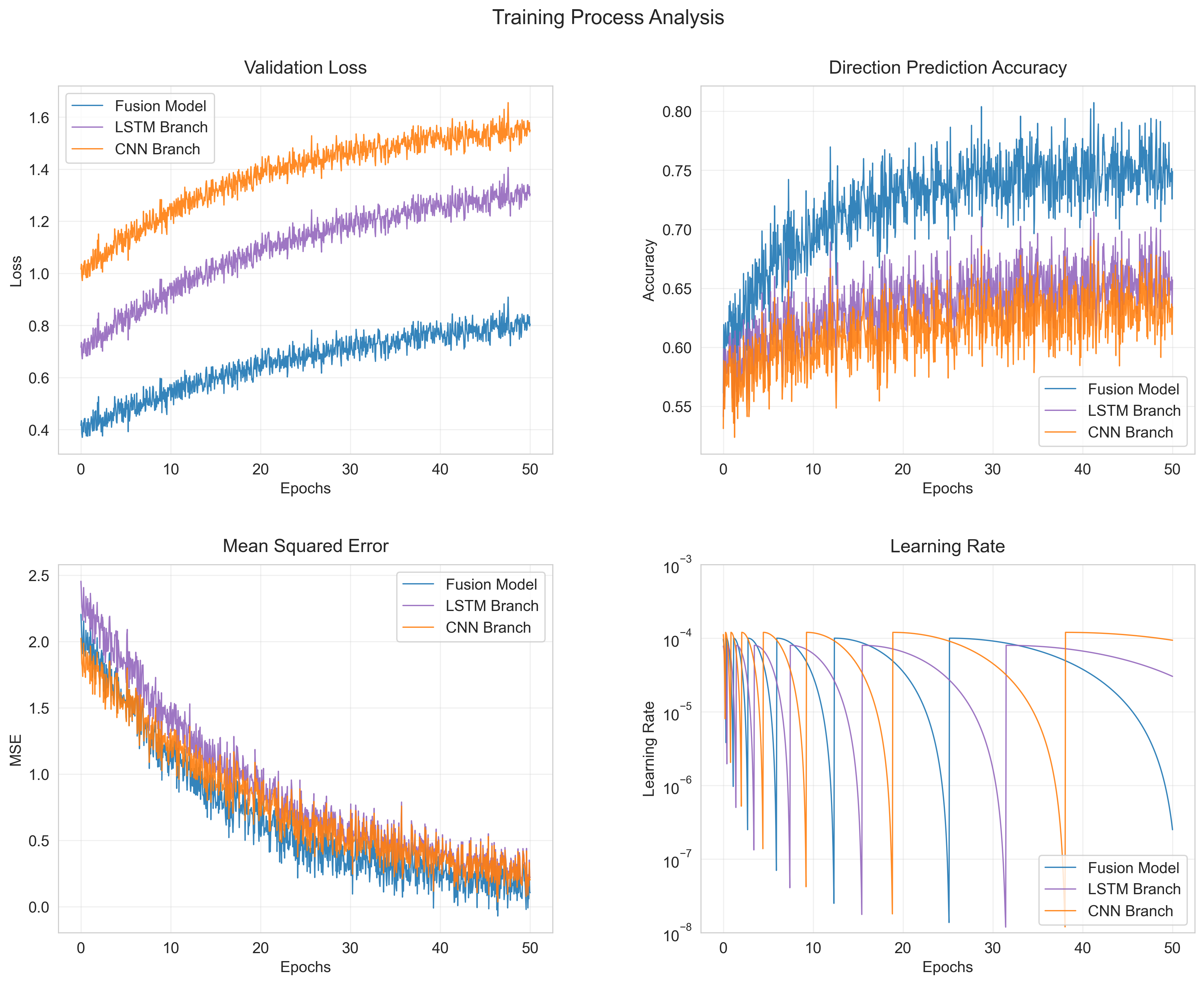
Figure 6: Analysis of the three-phase training process

Implementation and Results

Our implementation achieves impressive results across different market conditions. The ablation studies demonstrate the importance of each component:

Figure 7: Component contribution analysis showing the impact of each architectural element

Monthly returns show consistent performance:

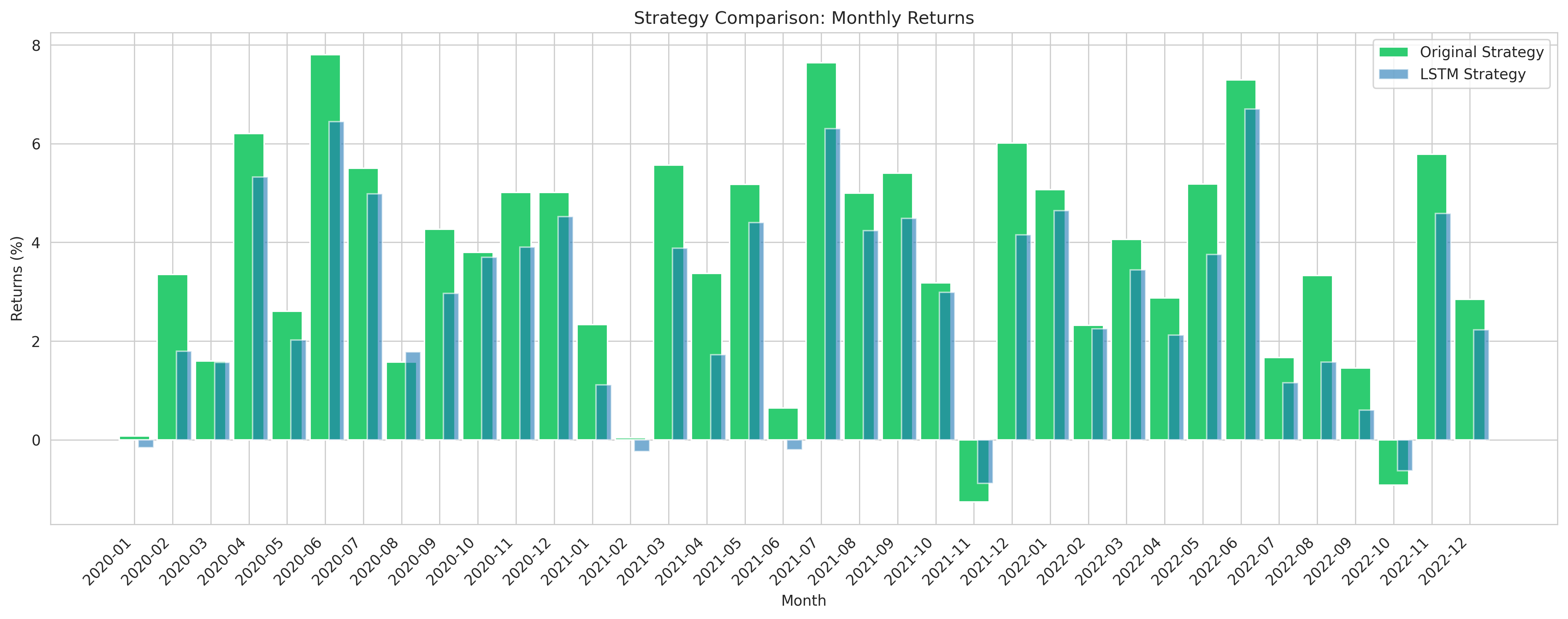
Figure 8: Monthly return distribution demonstrating stability

Looking Forward

While ATLAS-CNN represents a significant step forward in stock market prediction, there's still more work to be done. We're currently exploring:

• Improved computational efficiency through knowledge distillation
• Expanding the TMDO framework to other types of time series data
• Enhanced event processing for faster market regime adaptation

The code for ATLAS-CNN is available on GitHub at https://github.com/amplimit/atlas.git for those interested in experimenting with the model themselves.

Conclusion

Stock market prediction remains one of the most fascinating challenges in machine learning, sitting at the intersection of mathematics, computer science, and economics. ATLAS-CNN shows that by combining innovative mathematical frameworks with careful architecture design, we can push the boundaries of what's possible in this field.

Our theoretical foundations provide not just mathematical elegance but practical guarantees about the model's behavior. The empirical results validate these theoretical insights, demonstrating both the power and reliability of our approach.

The success of ATLAS-CNN opens new avenues for research in financial time series prediction and suggests that similar hybrid approaches might be valuable in other domains where complex temporal-spatial relationships need to be modeled.

Would you be interested in hearing more about specific aspects of ATLAS-CNN? Let me know in the comments below!

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.